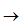Matematika Diskrit

Minggu, 23 September 2012

RELASI Matematika Diskrit

RELASI  

Jika di kehidupan nyata, ada yang namanya suatu hubungan (relasi) antara individu dan individu didalam suatu kelompok. Ataupun hubungan unsur lain terhadap unsur/ hal lain, misal, hubungan antar tetangga, hubungan mahasiswa dengan  mata kuliah ataupun hubungan dosen dengan pelajaran yang diampunya, dan lain-lain.

      Di materi Relasi ini, saya akan membahas tentang hubungan/ relasi, hubungan antara dua unsur/himpunan yang tidak kosong dengan satu aturan hubungan/perkaitan tertentu, Penjelasan yang saya akan jelaskan meliputi definisi dan fungsi, operasi dan sifatnya. 

Definisi

Kita misalkan E & F sebagai himpunan, hubungan antara himpunan E & himpunan F merupakan himpunan yang memiliki pasangan atau huruf/ angka yang berurutan,  tetapi  mengikuti aturan tertentu. Dengan demikian hubungan  biner R antar himpunan E dan F, merupakan himpunan  dari E × F / R ⊆(E × F).

Example:

Misal E  = {2, 4, 6} dan F = {2, 4, 6, 8 }. Jika didefinisikan relasi R dari E ke F  menggunakan aturan seperti, (e,fb) ∈ R jika faktor dari f, dan Seperti yang kalian pelajari sebelumnya atau yang sudah kalian ketahui,

 E × F menjadi :

E × F = {(2, 2), (2, 4), (2, 6), (2, 8), (4, 2), (4, 4), (4, 6), (4, 8), (6, 2), (6, 4), (6, 6), (6, 8)}

Jika menggunakan aturan relasi/ hubungan diatas, relasi R dari E  ke F  yang mengikuti aturan tadi menjadi,

R = {(2, 2), (2, 4), (2, 6), (2, 8)}

Hubungan/Relasi bisa juga  terjadi hanya pada satu atau sebuah himpunan, yaitu hubungan  pada E,  di himpunan E, yang merupakan himpunan E × E

Example: 

Misal R a/ relasi pada E = {2, 3, 4, 8, 9} yang diumpamakan :

(x, y) ∈ R dan bila x habis dapat dibagi oleh y.

Relasi R pada E  yang menggikuti aturan tersebut a/ seperti dibawah ini.

R = {(2, 2), (4, 4), (4, 2), (8, 8), (8, 2), (8, 4), (3, 3), (9, 9), (9, 3)}

Example about Relation/ contoh relasi : 

 

E :NAMA, SUBYEK/ Domain

F :OBYEK/ Kodomain

R :Relasi atau hubungan antar makanan favorit

                        Sifat-Sifat Relasi 

Relasi atau hubungan pada himpunan punya suatu sifat, sifat-sifat yang ada seperti..

1. Refleksif (reflexive)

Suatu relasi R pada himpunan E disebut refleksif jika (e, e) ∈ R untuk setiap e ∈ E. Dan bisa disebut juga hubungan relasi R pada himpunan E diketahui tidak refleksif jika e ∈ E dan begitu pula jika (a, a) ∉ R.

Example: 

Misalkan E = {1, 2, 3, 4}, 

dan sifat Relasi R adalah  ‘≤’ yang dimisalkan himpunan E, jadi

R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), 

(4, 4)}

Kelihatan bukan jika  (1, 1), (2, 2), (3, 3), (4, 4) adalah bagian unsur dari R. Jika begitu R dinyatakan himpunan Refleksif

Example : 

Misalkan E = {2, 3, 4, 8, 9, 15}.

Jika kita misalkan relasi R yang ada di himpunan A memiliki aturan:

(e, f) ∈ R jika e faktor prima dari f

Perlu diteliti/ diketahuin jika(4, 4) ∉ R .

Jadi, jelas bahwa R tidak  dan bukan bersifat refleksif.

Sifat refleksif memiliki ciri khas dalam pembuktian suatu relasi, seperti:

• Relasi yang memiliki sifat refleksif memiliki matriks dengan unsur utamanya semua bernilai 1, atau m_ii = 1, untuk i = 1, 2, …, n,

• Relasi yang memiliki sifat refleksif jika dibuktikan dalam bentuk graf terarah jadi  di graf tersebut akan ditemukan sebuah  loop pada setiap simpulnya.

2. Simetri (symmetric) dan Anti Simetri (antisymmetric)

Suatu relasi R di himpunan E memiliki sifat simetri jika 

(e, f) ∈ R, jika setiap e, f ∈ E , jadi (e, f) ∈ R.

Suatu relasi R pada himpunan E dikatakan tidak simetri jika (e,f) ∈ R sementara itu (e, f) ∉ R.

Pada suatu relasi R dihimpunan E mempunyai anti simetri dan misalkan untuk setiap

 a, b ∈ A, (a, b) ∈ R dan (b, a) ∈ R diakui jika a = b.

    Perhatikan bila istilah/ definisi simetri dan anti simetri bukanlah berlawanan, karena suatu relasi  bisa punya kedua sifat itu sekaligus. tapi , suatu relasi tak bisa mempunyai  kedua sifat itu jika dia punya atau memiliki pasangan berurutan atau terurut dengan bentuk

 (a, b) yang mana a ≠ b.

example: 

Misal R adalah sebuah relasi di himpunan Riil, yang dinyatakan oleh :

e R f  bila  & hanya jika e – f ∈ Y.

Memeriksa atau menyatakan relasi R memiliki sifat simetri !

Misal e R f  jadi/ maka (e – f) ∈ Y, Sementara  (f – e) ∈ Z.

Dan bila menyatakan seperti ini R memiliki sifat simetri.

Example : 

Buktikan bila relasi  ‘≤’ adalah himpunan Z.  Yang bersifat anti simetri

Jadi jika e ≤ f dan f ≤ e berarti e = f.

Hasilnya adalah  ‘≤’ menjadi/ memiliki sifat anti simetri.

3. Transitif (transitive)

Sebuah atau suatu relasi atau hubungan  R pada himpunan E mempunyai sifat transitif bila

(a, b) ∈ R dan (b, c) ∈ R, maka (a, c) ∈ R, untuk a, b, c ∈ A.

example :

Misal E  = { 2, 3, 4, 5, 6, 7, 8, 9}, & relasi  dapat diartikan bila :

e R f  jikalau & hanya bila e membagi f, dimana e, f ∈ E

Dan bila kita perhatikan definisi relasi R yang terdapat pada himpunan E, jadi :

R = {(2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6), (3, 9), (4, 4), (4, 8)}

Dan Bila (2, 4) ∈ R & (4, 8 ) ∈ R terbukti bila  (2, 8 ) ∈ R.

Dan relasi  R memiliki sifat transitif.

Example : 

R adalah relasi yang ada pada himpunan bilangan Riil N yang diketahui atau didefinisikan seperti:

R : E + f = 5, e, f ∈ E,

Dengan mengikuti relasi R pada himpunan E, jadi:

R = {(1, 4), (4, 1), (2, 3), (3, 2) }

Buktikan bila  (1, 4) ∈ R & (4, 1) ∈ R , terapi (1, 1) ∉ R.

Jika seperti ini relasi R bukan atau tidak memiliki sifat transitif.

Sifat transitif memiliki beberapa ciri didalam pembuktian satu relasi , misalkan, sifat transitif di graf yang terarah dinyatakan seperti:

Bila  ada  satu/ sebuah busur dari e ke f dan busur dari f  ke g, jadi  juga memiliki sebuah busur

Berarah/ diarahkan dari e ke g.

Dan saat/ bila  menyajikan suatu relasi transitif didalam bentuk matriks, sebuah relasi transitif tidak memiliki satu ciri khusus di matriksnya.

suku banyak

SUKU BANYAK

Rumus Suku Banyak Polinom Matematika

Rumus Web mengumpulkan materi Rumus Suku Banyak Polinom Matematika ini untuk anak SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan dipelajari

A. Suku Banyak (Polinom) adalah
Bentuk Umum :

dimana : adalah konstanta, n bilangan cacah.
Pangkat tertinggi x menyatakan derajat suku banyak.
Contoh :
B. Menghitung Suku Banyak/Nilai Suku Banyak
Misal :
Cara Menghitung :

1. Dengan Substitusi
Jika , maka nilai suku banyak tersebut x = -1 atau f (-1) .

2. Dengan pembagian sistem horner
Jika adalah suku banyak, maka f (h) diperoleh dengan cara berikut :

C. Pembagian Suku Banyak
Secara matematis dapat ditulis :

* Jika pembaginya fungsi linier, maka hasil bagi dan sisanya dapat dicari dengan cara metode pembagian sintetis Horner
* Jika pembaginya bukan linier dan tidak dapat diuraikan maka digunakan metode identitas.
Contoh:
Tentukan hasil bagi dan sisa pembagian suku banyak:dengan x -1 dengan menggunakan metode sintesis Horner!
Jawab :
Pembagian adalah (x-1), berarti k = 1
Kita gunakan metode sintetik berikut:

Dari bagan diatas terlihat bahwa hasil bagi adalah (x-1) dan sisa 40
D. Teorema Sisa

1. Suatu suku banyak f ( x ) jika dibagi ( x – a ) maka sisanya = f ( a )
2. Suatu suku banyak f( x ) jika dibagi ( x + a) maka sisanya f (-a)
3. Suatu suku banyak f ( x ) jika dibagi (ax – b) maka sisanya =
4. Suatu suku banyak f ( x ) habis dibagi (x – a) maka f (a) = 0

E. Teorema Faktor

1. Jika pada suku banyak f (x) berlaku f (a) = 0 dan f (b) = 0 maka f (c) = 0 maka f (x) habis dibagi (x – a)(x – b)(x – c).
2. Jika (x – a) adalah faktor dari f (x) maka x = a adalah akar dari f (x).
3. Jika f (x) dibagi oleh (x – a)(x – b) maka sisanya :
4. Jika f (x) dibagi oleh (x – a)(x – b)(x – c) maka sisanya : 

limit dan diferensial matematika

LIMIT & DIFERENSIAL dalam matematika

LIMIT
Dalam matematika, konsep limit digunakan untuk menjelaskan sifat dari suatu fungsi, saat argumen mendekati ke suatu titik, atau tak hingga; atau sifat dari suatu barisan saat indeks mendekati tak hingga. Limit dipakai dalam kalkulus (dan cabang lainnya dari analisis matematika) untuk mencari turunan dan kekontinyuan.
Dalam pelajaran matematika, limit biasanya mulai dipelajari saat pengenalan terhadap kalkulus, dan untuk memahami konsep limit secara menyeluruh bukan sesuatu yang mudah.


berarti f(x) dapat dibuat agar mempunyai nilai sedekat mungkin dengan L dengan cara membuat nilai x dekat dengan c. Dalam contoh ini, "limit dari f(x), bila x mendekati c, adalah L". Perlu diingat bahwa kalimat sebelumnya berlaku, meskipun f(c) L. Bahkan, fungsi f(x) tidak perlu terdefinisikan pada titik c. Kedua contoh dibawah ini menggambarkan sifat ini.
Sebagai contoh, pada saat x mendekati 2. Dalam contoh ini, f(x) mempunyai definisi yang jelas pada titik 2 dan nilainya sama dengan limitnya, yaitu 0.4:
f(1.9) f(1.99) f(1.999) f(2) f(2.001) f(2.01) f(2.1)
0.4121 0.4012 0.4001 0.4 0.3998 0.3988 0.3882
Semakin x mendekati 2, nilai f(x) mendekati 0.4, dan karena itu . Dalam kasus dimana , f disebut kontinyu pada x = c. Namun, kasus ini tidak selalu berlaku. Sebagai contoh,

Limit g(x) pada saat x mendekat 2 adalah 0.4 (sama seperti f(x)), namun ; g tidak kontinyu pada titik x = 2.
Atau, bisa diambil contoh dimana f(x) tidak terdefinisikan pada titik x = c.

Dalam contoh ini, pada saat x mendekati 1, f(x) tidak terdefinisikan pada titik x = 1 namun limitnya samadengan 2, karena makin x mendekati 1, f(x) makin mendekati 2:
f(0.9) f(0.99) f(0.999) f(1.0) f(1.001) f(1.01) f(1.1)
1.95 1.99 1.999 undef 2.001 2.010 2.10
Jadi, x dapat dibuat sedekat mungkin dengan 1, asal bukan persis sama dengan 1, jadi limit dari f(x) adalah 2.

Definisi formal
Sebuah limit didefinisikan secara formal sebagai berikut: Bila f adalah fungsi yang terdefinisikan pada sebuah interval terbuka yang mengandung titik c (dengan kemungkinan pengecualian pada titik c) dan L adalah bilangan real, maka

berarti bahwa untuk setiap terdapat yang untuk semua x dimana , berlaku .
Limit sebuah fungsi pada titik tak terhingga
Konsep yang berkaitan dengan limit saat x mendekati sebuah angka adalah konsep limit saat x mendekati tak terhingga, baik positif atau negatif. Ini bukan berarti selisih antara x dan tak terhingga menjadi kecil, karena tak terhingga bukanlah sebuah bilangan. Namun, artinya adalah x menjadi sangat besar (untuk tak terhingga) atau sangat kecil (untuk tak terhingga negatif).
Sebagai contoh, lihat .
• f(100) = 1.9802
• f(1000) = 1.9980
• f(10000) = 1.9998
Semakin x membesar, nilai f(x) mendekati 2. Dalam contoh ini, dapat dikatakan bahwa

Limit barisan
Perhatikan barisan berikut: 1.79, 1.799, 1.7999 ... Kita dapat mengamati bahwa angka-angka tersebut "mendekati" 1.8, limit dari barisan tersebut.
Secara formal, misalkan x1, x2, ... adalah barisan bilangan riil. Kita menyebut bilangan riil L sebagai limit barisan ini dan menuliskannya sebagai

yang artinya
Untuk setiap bilangan riil ε > 0, terdapat sebuah bilangan asli n0 sehingga untuk semua n > n0, |xn − L| < ε.
Secara intuitif ini berarti bahwa pada akhirnya semua elemen barisan tersebut akan mendekat sebagaimana yang kita kehendaki terhadap limit, karena nilai absolut |xn − L| adalah jarak antara x dan L. Tidak semua barisan memiliki limit. Bila ada, kita menyebutnya sebagai konvergen, bila tidak, disebut divergen. Dapat ditunjukkan bahwa barisan konvergen hanya memiliki satu limit.
Limit barisan dan limit fungsi berkaitan erat. Pada satu sisi, limit barisan hanyalah limit pada tak terhingga dari suatu fungsi yang didefinisikan pada bilangan asli. Di sisi lain, limit sebuah fungsi f pada x, bila ada, sama dengan limit barisan xn = f(x + 1/n).


LANGKAH MENCARI LIMIT SUATU FUNGSI

1. Harga yang didekati disubstitusikan ke fungsi yang dimaksud.
Bila bukan (*) maka itulah nilai limitnya.
2. Bila (*) maka usahakan diuraikan.
Pada fungsi pecahan, faktor yang sama pada pembilang dan penyebut (penyebab bentuk (*)) dicoret. Pencoretan im boleh dilakukan, karena x hanya mardekati harga yang diberikan. Kemudian baru harga yang didekati disubstitusikan. Dalam konteks limit perhatikan hasil pembagian berikut :

0/a = 0 ; a/0 =  ; /a =  ; a/ = 0 ; ± a =konstanta)

KETENTUAN

Untuk x <<< ( x  0 ) maka sin x x
(x <<< kecil sekali ;  setara )

l i m sin x = 1 l i m tg x = 1
x  0 x x  0 x
l i m x = 1 l i m x = 1
x  0 sin x x  0 tg x
PERLUASAN
l i m sin ax = a/b l i m tg ax = a/b
x  0 bx x  0 bx

l i m ax = a/b l i m ax = a/b
x  0 sin bx x  0 tg bx

l i m sin ax = a/b l i m tg ax = a/b
x  0 sin bx x  0 tg bx


l i m sin ax = a/b l i m tg ax = a/b
x  0 tg bx x  0 sin bx
Rumus-rumus trigonometri yang sering digunakan untuk merubah fungsi:

cos x = sin (90° - x)
ctg x = tg (90° - x)
sin ax = 2 sin ½ax cos ½ax
cos ax = 1- 2 sin² ½ax
cos²x = 1 - sin²x


HAL-HAL KHUSUS
l i m axm + bxm-1 + .... =
x  pxn + qxn-1 + ...  untuk m > n ;
a/p untuk m =n ;
0 untuk m < n

l i m ax2 + bx + c - dx2 + ex + f
x   untuk a > d ;
b-e untuk m =n ;
2a
- untuk a < d
Bila salah satu suku belum berbentuk tanda akar maka dibentuk dengan cara mengkuadratkan kemudian menarik tanda akar.


DALIL L'HOSPITAL

Jika fungsi f dan g masing-masing terdifferensir pada titik x= a
dan f(a) = g(a) = 0 atau f(a) = g(a) =  maka

l i m f(x) = l i m f(x)
x  g(x) x a g(x)


CONTOH LIMIT FUNGSI ALJABAR

1. l i m x2 - 5x + 6 = (3)2 - 5(3) + 6 = 0
x 3

2. l i m 3x - 2 =  (*) Uraikan
x  2x + 1 

x(3 - 2/x) = 3 - 2/x = 3 - 0 = 3
x(2 - 1/x) 2 + 1/x 2 - 0 2

atau langsung gunakan hal khusus

3. l i m x2 - x - 1 =  (*) Uraikan
x  10x + 9 

x(x - 1 - 1/x) = x - 1 - 1/x =  - 1 - 0 =  =
x(10 - 9/x) 10 + 9/x 10 + 0 10

atau langsung gunakan hal khusus


4. l i m x2 - 3x + 2 = 0 (*) Uraikan
x 2 x2 - 5x + 6 0

(x - 1)(x - 2) = (x - 1) = 2 - 1 = -1
(x - 3)(x - 2) = (x - 3) = 2 - 3

atau langsung gunakan hal khusus  Differensial


5. l i m x3 - 3x2 + 3x - 1 = 0 (*) Uraikan
x 1 x2 - 5x + 6 0

(x - 1)3 = (x - 1)2 = (1 - 1)2 = 0
(x - 1) (x - 5) (x + 5) (1 + 5) 6

atau langsung gunakan hal khusus  Differensial



6. l i m 2 + x - 2x = 0 (*) Hilangkan tanda akar dengan
x 2 x - 2 0 mengalikan bentuk sekawan

(x - 1)3 = (x - 1)2 = (1 - 1)2 = 0 = 0
(x - 1) (x - 5) (x + 5) (1 + 5) 6

atau langsung gunakan hal khusus  Differensial



7. l i m (3x - 9x2 + 4x) =  -  (*) Hilangkan tanda akar
x 

l i m (3x - 9x2 + 4x ) =  3x - 9x2 + 4x  = (*) Hilangkan tanda
x   3x - 9x2 + 4x  akar
l i m (9x2 - (9x2 + 4x) = l i m -4x =
x  3x + (9x2 + 4x) x  3x + 3x [1+(a/9x)]

l i m -4 = -4 = -2
x  3 + 3(1 + 0) 6 3

atau langsung gunakan hal khusus

CONTOH LIMIT FUNGSI TRIGONOMETRI
1. l i m sin 2x = 0 (*)
x 0 tg 3x 0
sin 2x = 3x 2 = 1 . 1 . 2 = 2
2x tg 3x 3 3 3
2. l i m 1 - cos 2x = 0
x 0 sin 2x 0
1 - (1 - 2 sin² 2x) = 2 sin² x = sin x = tg x = 0
2 sin x cos x 2 sin x cos cos x
3. l i m 1 - cos x = 0
x 0 3x² 0
2 sin² (½x) = sin (½x) . sin (½x) = 1 . 1 . 1 = 1
3 . 4 . (½x) 6 (½x) (½x) 6 6
atau langsung gunakan hal khusus  Differensial
4. l i m sin x - sin a = 0 (*)
x 0 x - a 0
2 cos ½(x+a) sin ½(x-a) = cos ½(x+a) . sin ½(x-a) =
x - a ½ (x - a )
cos ½(x+a) . 1 = cos ½(a+a) . 1 = cos a
DIFERENSIAL
Kalkulus diferensial adalah salah satu cabang kalkulus dalam matematika yang mempelajari bagaimana nilai suatu fungsi berubah menurut perubahan input nilainya. Topik utama dalam pembelajaran kalkulus diferensial adalah turunan. Turunan dari suatu fungsi pada titik tertentu menjelaskan sifat-sifat fungsi yang mendekati nilai input. Untuk fungsi yang bernilai real dengan variabel real tunggal, turunan pada sebuah titik sama dengan kemiringan dari garis singgung grafik fungsi pada titik tersebut. Secara umum, turunan suatu fungsi pada sebuah titik menentukan pendekatan linear terbaik fungsi pada titik tersebut.


Grafik dari sebuah fungsi (garis hitam) dan sebuah garis singgung terhadap fungsi (garis merah). Kemiringan garis singgung sama dengan turunan dari fungsi pada titik singgung
Proses pencarian turunan disebut pendiferensialan (differentiation). Teorema dasar kalkulus menyatakan bahwa pendiferensialan adalah proses keterbalikan dari pengintegralan.
Turunan mempunyai aplikasi dalam semua bidang kuantitatif. Di fisika, turunan dari perpindahan benda terhadap waktu adalah kecepatan benda, dan turunan dari kecepatan terhadap waktu adalah percepatan. Hukum gerak kedua Newton menyatakan bahwa turunan dari momentum suatu benda sama dengan gaya yang diberikan kepada benda.
Laju reaksi dari reaksi kimia juga merupakan turunan. Dalam riset operasi, turunan menentukan cara paling efisien dalam memindahkan bahan dan mendesain pabrik. Dengan menerapkan teori permainan, turunan dapat memberikan strategi yang paling baik untuk perusahaan yang sedang bersaing.
Turunan sering digunakan untuk mencari titik ekstremum dari sebuah fungsi. Persamaan-persamaan yang melibatkan turunan disebut persamaan diferensial dan sangat penting dalam mendeskripsikan fenomena alam. Turunan dan perampatannya (generalization) sering muncul dalam berbagai bidang matematika, seperti analisis kompleks, analisis fungsional, geometri diferensial, dan bahkan aljabar abstrak.
Misalkan x dan y adalah bilangan real di mana y adalah fungsi dari x, yaitu y = f(x). Salah satu dari jenis fungsi yang paling sederhana adalah fungsi linear. Ini adalah grafik fungsi dari garis lurus. Dalam kasus ini, y = f(x) = m x + c, di mana m dan c adalah bilangan real yang tergantung pada garis mana grafik tersebut ditentukan. m disebut sebagai kemiringan dengan rumus:

di mana simbol Δ (delta) memiliki arti "perubahan nilai". Rumus ini benar adanya karena
y + Δy = f(x + Δx) = m (x + Δx) + c = m x + c + m Δx = y + mΔx.
Diikuti pula Δy = m Δx.
Namun, hal-hal di atas hanya berlaku kepada fungsi linear. Fungsi nonlinear tidak memiliki nilai kemiringan yang pasti. Turunan dari f pada titik x adalah pendekatan yang paling baik terhadap gagasan kemiringan f pada titik x, biasanya ditandai dengan f'(x) atau dy/dx. Bersama dengan nilai f di x, turunan dari f menentukan pendekatan linear paling dekat, atau disebut linearisasi, dari f di dekat titik x. Sifat-sifat ini biasanya diambil sebagai definisi dari turunan.
Sebuah istilah yang saling berhubungan dekat dengan turunan adalah diferensial fungsi.

Garis singgung pada (x, f(x))
Bilamana x dan y adalah variabel real, turunan dari f pada x adalah kemiringan dari garis singgung grafik f' di titik x. Karena sumber dan target dari f berdimensi satu, turunan dari f adalah bilangan real. Jika x dan y adalah vektor, maka pendekatan linear yang paling mendekati grafik f tergantung pada bagaimana f berubah di beberapa arah secara bersamaan. Dengan mengambil pendekatan linear yang paling dekat di satu arah menentukan sebuah turunan parsial, biasanya ditandai dengan ∂y/∂x. Linearisasi dari f ke semua arah secara bersamaan disebut sebagai turunan total. Turunan total ini adalah transformasi linear, dan ia menentukan hiperbidang yang paling mendekati grafik dari f. Hiperbidang ini disebut sebagai hiperbidang oskulasi; ini secara konsep sama dengan mengambil garis singgung ke semua arah secara bersamaan.
2. Penerapan turunan
2. 1. Optimalisasi
Jika f adalah fungsi yang dapat diturunkan pada R (atau interval terbuka) dan x adalah maksimum lokal ataupun minimum lokal dari f, maka turunan dari f di titik x adalah nol; titik-titik di mana f '(x) = 0 disebut titik kritis atau titik pegun (dan nilai dari f di x disebut nilai kritis). (Definisi dari titik kritis kadang kala diperluas sampai meliputi titik-titik di mana turunan suatu fungsi tidak eksis.) Sebaliknya, titik kritis x dari f dapat dianalisa dengan menggunakan turunan ke-dua dari f di x:
• jika turunan ke-dua bernilai positif, x adalah minimum lokal;
• jika turunan ke-dua bernilai negatif, x adalah maksimum lokal;
• jika turunan ke-dua bernilai nol, x mungkin maksimum lokal, minimum lokal, ataupun tidak kedua-duanya. (Sebagai contohnya, f(x)=x³ memiliki titik kritis di x=0, namun titik itu bukanlah titik maksimum ataupun titik minimum; sebaliknya f(x) = ±x4 mempunyai titik kritis di x = 0 dan titik itu adalah titik minimum maupun maksimum.)
Ini dinamakan sebagai uji turunan ke dua. Sebuah pendekatan alternatif lainnya, uji turunan pertama melibatkan nilai f ' di kedua sisi titik kritis.
Menurunkan fungsi dan mencari titik-titik kritis biasanya merupakan salah satu cara yang sederhana untuk mencari minima lokal dan maksima lokal, yang dapat digunakan untuk optimalisasi. Sesuai dengan teorema nilai ekstremum, suatu fungsi yang kontinu pada interval tertutup haruslah memiliki nilai-nilai minimum dan maksimum paling sedikit satu kali. Jika fungsi tersebut dapat diturunkan, minima dan maksima hanya dapat terjadi pada titik kritis atau titik akhir.
Hal ini juga mempunyai aplikasi tersendiri dalam proses sketsa grafik: jika kita mengetahui minima dan maksima lokal dari fungsi yang dapat diturunkan tersebut, sebuah grafik perkiraan dapat kita dapatkan dari pengamatan bahwa ia akan meningkat dan menurun di antara titik-titik kritis.
Di dimensi yang lebih tinggi, titik kritis dari nilai skalar fungsi adalah titik di mana gradien fungsi tersebut adalah nol. Uji turunan kedua masih dapat digunakan untuk menganalisa titik-titik kritis dengan menggunakan eigennilai matriks Hessian dari turunan parsial ke-dua fungsi di titik kritis. Jika semua eigennilai tersebut adalah positif, maka titik tersebut adalah minimum lokal; jika semuanya negatif, maka titik itu adalah maksimum lokal. Jika ada beberapa yang positif dan beberapa yang negatif, maka titik kritis tersebut adalah titik pelana, dan jika tidak ada satupun dari keadaan di atas yang terpenuhi (misalnya ada beberapa eigennilai yang nol) maka uji tersebut inkonklusif.
Kalkulus variasi
Salah satu contoh masalah optimalisai adalah mencari kurva terpendek anatar dua titik di atas sebuah permukaan dengan asumsi kurva tersebut harus berada di permukaan tersebut. Jika permukaan tersebut adalah bidang rata, maka kurva yang paling pendek berupa garis lurus. Namun jika permukaannya tidak bidang, maka kita tidak bisa mengetahui secara pasti kurva yang paling pendek. Kurva ini disebut sebagai geodesik, dan salah satu masalah paling sederhana di kalkulus variasi adalah mencari geodesik.Contoh lainnya adalah mencari luas permukaan paling kecil yang dibatasi oleh kurva tertutup di ruang tiga dimensi. Permukaan ini disebut sebagai permukaan minimum, dan ini dapat dicari dengan menggunakan kalkulus variasi.
Persamaan diferential
Persamaan diferensial adalah hubungan antara sekelompok fungsi dengan turunan-turunannya. Persamaan diferensial biasa adalah sebuah persamaan diferensial yang menghubungkan fungsi dengan sebuah variabel ke turunannya terhadap variabel itu sendiri. Persamaan diferensial parsial adalah persamaan diferensial yang menghubungkan fungsi yang memiliki lebih dari satu variable ke turunan parsialnya. Persamaan diferensial muncul secara alami dalam sains fisik, model matematika, dan dalam matematika itu sendiri. Sebagai contoh, Hukum kedua Newton yang menggambarkan hubungan antara percepatan dengan posisi dapat dimulai dengan persamaan diferensial biasa:

Persamaan kalor di variable satu ruang yang menggambarkan bagaimana kalor dapat berdifusi melalui satu tongkat yang lurus adalah persamaan diferensial parsial

Di sini u(x, t) adalah temperatur tongkat pada posisi x dan waktu t dan α adalah sebuah tetapan yang bergantung pada seberapa cepat kalor tersebut berdifusi.


Differensial (turunan) fungsi y = f(x) terhadap x didefinisikan sebagai :

dy = l i m f(x + x) - f(x)
dx x  0 x

(Perbandingan perubahan y yang disebabkan karena perubahan x, untuk perubahan x yang kecil sekali)

Notasi lain : df/dx = f`(x) ; y`

RUMUS - RUMUS
1. FUNGSI ALJABAR
y = xn  dy/dx = nxn-1 2. FUNGSI TRIGONOMETRI
y = sin x  dy/dx = cos x
y = cos x  dy/dx = - sin x
y = sin x  dy/dx = sec²x
Sifat - sifat :

1. y = c (c=konstanta)  dy/dx = 0

2. y = c U(x)  dy /dx = c . U`(x)

3. y = U(x) ± V(x)  dy /dx = U`(x) ± V`(x)

4. Bentuk perkalian
y = U(x) . V(x)  dy/dx = U`(x).V(x) + U(x).V`(x)

5. Bentuk pembagian
y = U(x)  dy = U`(x).V(x) - U(x).V`(x)
V(x) dx (V(x))²

6. Bentuk rantai
y = f(U) dan U = g(x)  dy/dx = dy/du .du/dx

y = (ax + b)n
dy/dx = n(ax+b)n-1(a)

y = sin (ax + b)
dy/dx = (a) cos (ax+b)

y = sinn (ax + b)
dy/dx = n sinn-1(ax+b) [a cos (ax+b)]

Ket : Untuk menyelesaikan persoalan, sifat dan rumus-rumus ini dikombinasikan



1. MENENTUKAN KOEFISIEN ARAN GARIS SINGGUNG
(Gradien) di titik (x1y1) pada kurva y = f(x)

f`(x1) berarti nilai turunan f(x) pada titik dengan absis x = x1,

Ket:
Khusus untuk jenis fungsi kuadrat. Jika titik tidak terletak pada grafik, maka gradien garis singgungnya dimisalkan dengan m yang dicari dengan menggunakan persamaan garis y - y1 = m (x - x1) disinggungkan dengan persamaan kurva y = f(x) dengan syarat D = 0 (D = diskriminan dari hasil eliminasi kedua persamaan)
2. MENENTUKAN MONOTON FUNGSI

• Fungsi y = f(x) monoton naik pada suatu interval,
jika pada interval itu berlaku f'(x) > 0

• Fungsi y = f(x) monoton turun pada suatu interval,
jika pada interval itu berlaku f'(x) < 0
3. MENENTUKAN TITIK STASIONER

Fungsi y = f(x)  Syarat stasioner f'(x) = 0

JENIS - JENISNYA

STASIONER :

MAKSIMUM
Syarat : f`(x) = 0  x = x0; f'' (x0) < 0  Titik maksimum (xo, f(xo))

MINIMUM
Syarat : f '(x) = 0  x = x0; f'' (x0) > 0 Titik Minimum (xo, f(xo))

BELOK
Syarat : f '(x) = 0  x = x0; f'' (x0) = 0 Titik belok (xo, f(xo))

Nilai Stasioner adalah nilai fungsi di absis titik stasioner

Keterangan :
1. Untuk menentukan jenis jenis titik stasioner dapat juga dicari dengan melihat perubahan tanda disekitar titik stasioner.
Langkah :
a. Tentukan absis titik stasioner dengan syarat f '(x) = 0 x = xo
b. Buat garis bilangan f '(x)
c. Tentukan tanda-tanda disekitar titik stasioner dengan mensubstitusi sembarang titik pada f '(x)
d. Jenis titik stasioner ditentukan oleh perubahan tanda di sekitar
titik stasioner.
ket : f`(x) > 0 grafik naik
f`(x) > 0 grafik turun

2. Nilai maksimum/minimum suatu fungsi dalam interval tertutup didapat dari nilai stasioner fungsi dalam interval itu atau dari nilai fungsi pada ujung - ujung interval

soal dan jawaban statistika

1. Tentukan datum terkecil, datum terbesar, median, kuartil bawah, dan kuartil atas dari data berikut:
a. 8, 7, 9, 4, 6, 5, 4
b. 9, 8, 7, 9, 4, 6, 5, 4
Jawab:
a. Banyak data (n) sama dengan 7. Jika data ini diurutkan dari yang terkecil, diperoleh

No. Urut Data	X1	X2	X3	X4	X5	X6	X7
Nilai Data	4	4	5	6	7	8	9

• Datum terkecil adalah x₁ = 4.
• Datum terbesar adalah x₇ = 9.
• Median merupakan datum tengah setelah data diurutkan. Jadi, median (Q₂) = x₄ = 6. Jika menggunakan rumus

• Kuartil bawah (Q₁)
Q₁ = median dari 4 4 5
Jadi, Q₁ = 4 (nilai paling tengah)
• Kuartil atas (Q₃)
Q₃ = median dari 7 8 9
Jadi, Q₃ = 8 (nilai paling tengah)
b. Banyak datum (n) sama dengan 8. Jika data diurutkan, diperoleh

No. Urut Data	X1	X2	X3	X4	X5	X6	X7
Nilai Data	4	4	5	6	7	8	9

• Datum terkecil adalah x₁ = 4.
• Datum terbesar adalah x₈ = 9.
Median tidak dapat ditentukan dengan cara seperti soal (a). Median untuk data genap (n = 8) ditentukan dengan menggunakan rumus sebagai berikut.

Dengan cara yang sama, diperoleh Q₁ = 4,5 dan Q₃ = 8,5.
2. Hasil dari suatu pengamatan adalah sebagai berikut.
12 11 9 8 9 10 9 12
Median dari pengamatan tersebut adalah ….
Jawab:
Data diurutkan dari yang terkecil.
8 9 9 9 10 11 12 12
Mediannya adalah (9+10)/2 = 9,5
3. Seorang peneliti mengambil masing-masing 1 kg air dari 20 sungai yang berbeda untuk diuji kadar garamnya. Hasil pengujian (dalam mg) adalah
193 282 243 243 282 214 185 128 243 159
218 161 112 131 201 132 194 221 141 136
Dari data tersebut tentukan:
a. jangkauan data;
b. jangkauan antarkuartil;
c. simpangan kuartil.
Jawab:
Data diurutkan hasilnya sebagai berikut:

trigonometri

Rumus trigonometri umum Sudut-Sudut Istimewa sin cos tan 0 30 45 60 90 derajat Aturan sin cos tan lain Rumus-rumus Trigonometri pada segitiga dengan sisi a b c Aturan sinus Aturan Cosinus Luas Segitiga 2 sisi dan 1 sudut Luas segitiga dengan 3 sisi akan dibahas lain waktu Rumus jumlah 2 sudut trigonometri sin cos tan sepertinya gambar ini ada yang salah, nanti diperbaiki Sudut 2A atau sin 2x, cos 2x, tan 2x Rumus kali trigonometri sin cos cos sin cos cos -sin sin Rumus jumlah 2 trigonometri sin cos cos sin cos cos -sin sin Persamaan Trigonometri mudah sekali dikerjakan Bentuk a Cos x + b Sin x = k cos x-teta Bentuk a Cos x + b Sin x = c Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x

TRANSLASI

GEOMETRI TRANSFORMASI

1. Pengertian Transformasi Transformasi T dibidang adalah suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. 
Jenis-jenis transformasi yang dapat dilakukan antara lain :

1. Translasi (Pergeseran)
2. Refleksi (Pencerminan)
3. Rotasi (Perputaran)
4. Dilatasi (Perkalian)

2. Translasi dan Operasinya
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu. 
Jika translasi  memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk : 

 
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi 
Jawab : 

Jawab :

A’ = ( -3 + 3, 4 + 6)

A’ = (0, 10)

3. Refleksi (Pencerminan) 

a. Pencerminan terhadap sumbu x

Matriks percerminan :

b. Pencerminan Terhadap sumbu y 

Matriks Pencerminan:

c. Pencerminan terhadap garis y = x 

Matriks Pencerminan

d. Pencerminan terhadap garis y = -x 

Matriks Pencerminan:

e. Pencerminan terhadap garis x = h 

Matriks Pencerminan: 

Sehingga:

f. Pencerminan terhadap garis y=k 

Matriks Pencerminan : 

Sehingga:

g. Pencerminan terhadap titik asal O (0, 0)

Matriks Pencerminan : 

Sehingga: 

h. Pencerminan terhadap garis y = mx dimana m = tan q

Contoh :

Tentukan bayangan persamaan garis y = 2x – 5 oleh translasi 

Jawab :

Ambil sembarang titik pada garis y = 2x – 5, misalnya (x, y) dan titik bayangan oleh translasi  adalah (x’, y’) sehingga ditulis 

Atau

x’ = x + 3 x = x’- 3 ..... (1)

y’ = y – 2  y = y’ + 2 ......(2)

Persamaan (1) dan (2) disubtitusikan pada persamaan garis semula, sehingga :

y = 2x – 5

y’ + 2 = 2 (x’- 3) – 5

y’ = 2x’ – 6 – 5 – 2

y’ = 2x’ – 13

Jadi persamaan garis bayangan y = 2x – 5 oleh translasi adalah y = 2x – 13 .